Primary & secondary rainbow supernumeraries - OPOD
Primary & Secondary Rainbow Supernumeraries: An Intriguing Phenomenon
Rainbows have captivated the human imagination for centuries with their vibrant colors and ethereal beauty. While most of us are familiar with the primary and secondary rainbows, there is a fascinating optical phenomenon associated with these rainbows that often goes unnoticed – supernumeraries. These delicate fringes of light, also known as supernumerary bows, add an extra touch of magic to the already enchanting spectacle of rainbows.
Discovering Supernumeraries
Supernumeraries were given their name because they were initially considered "extras" that shouldn't exist. In fact, classical ray theory, popularized by Descartes and Newton's corpuscular theory of light, failed to explain their presence. It wasn't until Thomas Young introduced the concept of waves in 1803 that an explanation for the existence of supernumeraries began to emerge.
The Work of George Biddell Airy
In 1836, George Biddell Airy, the Astronomer Royal, provided a quantitative treatment of supernumeraries that still holds true today. His work laid the foundation for accurate predictions and understanding of these elusive phenomena. Airy's calculations, based on wave theory, shed light on the intricate interplay of light waves and droplet size that give rise to supernumeraries.
The Role of Droplet Size
To observe supernumeraries, specific conditions must be met. Rain droplets of uniform size are crucial in producing these rare sights. The droplets need to be very similar in size to create the pronounced angular oscillations in brightness that characterize primary supernumeraries. Secondary supernumeraries, on the other hand, are seen less frequently due to the wider spacing between fringes and the minimal variation in brightness.
Simulating Supernumeraries
Thanks to advancements in technology, we can now simulate the formation of supernumeraries with great accuracy. Mie-Lorentz calculations, developed after 1908, have proven to be highly reliable in generating simulations that closely match observed phenomena. These calculations consider the scattering of light waves by droplets and accurately reproduce the brightness inside the primary bow and the darkness of Alexander's dark band between the primary and secondary rainbows.
The Elusive Secondary Supernumeraries
While primary supernumeraries are relatively more common and easily observed, secondary supernumeraries remain a rare sight. This rarity can be attributed to the delicate balance of viewing angle and wavelength that determines whether the wave crests coincide or are out of phase. When the wave crests align, a bright arc, or a secondary supernumerary bow, is formed. Due to the wider spacing between fringes and minimal variation in brightness, secondary supernumeraries are often unknowingly photographed but less frequently noticed by the naked eye.
A Visual Representation
To visualize the formation of supernumeraries, a simulation adapted from Philip Laven's MiePlot provides a clear depiction. The simulation shows how primary supernumeraries are closely spaced with pronounced angular oscillations in brightness. In contrast, secondary supernumeraries are widely spaced, and there is little variation in brightness between each fringe. This visual representation helps us understand the intricate interplay of light waves and droplet size that gives rise to these mesmerizing optical phenomena.
In conclusion, primary and secondary rainbow supernumeraries add an extra layer of intrigue and beauty to the already captivating spectacle of rainbows. Understanding the role of droplet size, wave theory, and viewing angles helps demystify these phenomena that were once considered extras in the realm of atmospheric optics. The work of George Biddell Airy and advancements in simulation techniques have allowed us to delve deeper into the science behind these elusive fringes of light. So, the next time you witness a rainbow gracing the sky, take a moment to appreciate the subtle wonders of primary and secondary rainbow supernumeraries.

Atmospheric
Optics
About - SubmitOptics Picture of the DayGalleriesPreviousNextToday



_OpticsPOD - Optics Picture of the Day - OPOD | Today - Galleries - Submit Image - _Atmospheric Optics
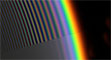
Supernumeraries
Primary and secondary bow supernumerary fringes imaged by Douglas Booth.
He saw these near sunset rainbows on the island of Berneray in the Outer Hebrides off the west coast of Scotland.
To the right and inside the primary bow there are 4-5 fringes.
At left is a much more rare sight, 2-3 secondary supernumerary fringes or bows.
Image ©Douglas Booth

A colour subtraction enhancement showing the many fringes.
Small rain droplets of quite uniform size were needed to produce this rare sight.
Supernumeraries probably became so named because they were 'extras' and not supposed to exist. Classical ray theory as used by Descartes to explain the rainbow cannot account for them. The problem was further compounded by long insistence on Newton's corpuscular theory of light.
We need waves. They were used by Thomas Young in 1803 to explain supernumerary existence.
Astronomer Royal, George Biddell Airy produced a quantitative treatment in 1836 that still provides fully workable predictions.
Mie-Lorentz calculations (after 1908) are wholly accurate and were used to generate the page background simulation.
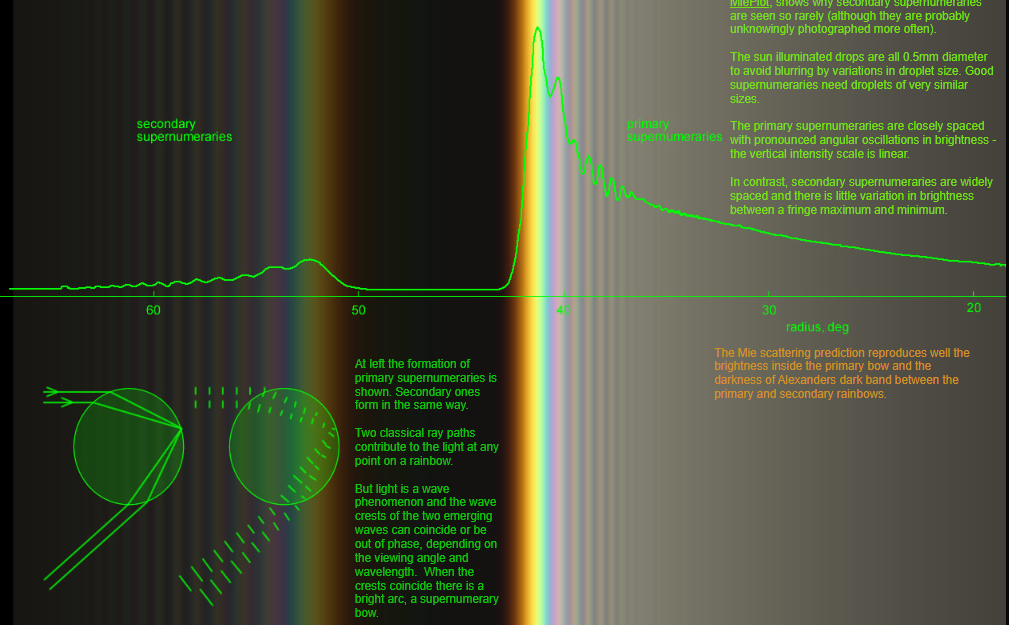
This simulation, adapted from Philip Laven's MiePlot, shows why secondary supernumeraries are seen so rarely (although they are probably unknowingly photographed more often).
The sun illuminated drops are all 0.5mm diameter to avoid blurring by variations in droplet size. Good supernumeraries need droplets of very similar sizes.
The primary supernumeraries are closely spaced with pronounced angular oscillations in brightness - the vertical intensity scale is linear.
In contrast, secondary supernumeraries are widely spaced and there is little variation in brightness between a fringe maximum and minimum.
At left the formation of primary supernumeraries is shown. Secondary ones form in the same way.
Two classical ray paths contribute to the light at any point on a rainbow.
But light is a wave phenomenon and the wave crests of the two emerging waves can coincide or be out of phase, depending on the viewing angle and wavelength. When the crests coincide there is a bright arc, a supernumerary bow.
The Mie scattering prediction reproduces well the brightness inside the primary bow and the darkness of Alexanders dark band between the primary and secondary rainbows.
Note: this article has been automatically converted from the old site and may not appear as intended. You can find the original article here.
Reference Atmospheric Optics
If you use any of the definitions, information, or data presented on Atmospheric Optics, please copy the link or reference below to properly credit us as the reference source. Thank you!
-
<a href="https://atoptics.co.uk/blog/primary-secondary-rainbow-supernumeraries-opod/">Primary & secondary rainbow supernumeraries - OPOD</a>
-
"Primary & secondary rainbow supernumeraries - OPOD". Atmospheric Optics. Accessed on April 28, 2024. https://atoptics.co.uk/blog/primary-secondary-rainbow-supernumeraries-opod/.
-
"Primary & secondary rainbow supernumeraries - OPOD". Atmospheric Optics, https://atoptics.co.uk/blog/primary-secondary-rainbow-supernumeraries-opod/. Accessed 28 April, 2024
-
Primary & secondary rainbow supernumeraries - OPOD. Atmospheric Optics. Retrieved from https://atoptics.co.uk/blog/primary-secondary-rainbow-supernumeraries-opod/.