OPOD - Topology & Mirages

Last updated on September 16, 2023

OPOD - Topology & Mirages: A Fascinating Insight into Mirage Structure

Mirages have long captivated our imagination with their mesmerizing illusions. They are optical phenomena that occur when light rays bend as they pass through layers of air with different temperatures. While we are familiar with the basic concept of mirages, there is a deeper understanding of their structure and behavior that can be explored through the lens of topology. In this article, we will delve into the fascinating world of mirages and how topology provides unique insights into their formation.

Unraveling the Complexity of Mirages

Let's begin by examining a remarkable mirage captured by Mark Evans over the dry estuary sands of Swansea Bay, Wales. The image reveals multiple distorted reflections of gas storage tanks located 7 kilometers away. What makes this mirage particularly intriguing is the presence of both inverted and erect images, alternating in a pattern that defies conventional expectations.

To comprehend the complexity of this mirage, we can turn to the concept of topology. Topology represents mirages as images pasted on an inner "image sphere," with the actual objects pasted on a larger "object sphere." By smoothly expanding and distorting the inner sphere, mirage images can be transformed to match the object, resulting in a continuous and congruent overlay.

Unveiling the Mirage Structure

The mirage captured by Mark Evans showcases a series of sloping steps around one of the tanks. These steps alternate in direction, with some sloping downwards from right to left and others in the opposite direction. In a typical "inferior mirage," where a single inverted image appears below the object, such variations in slope would not be expected. However, this mirage presents an unusually complete inferior mirage due to the undulating warm sands that have tilted the boundaries between temperature layers.

Topology plays a crucial role in explaining the presence of multiple images and their alternating orientation. By mentally manipulating the rubbery spheres representing the mirage, we can derive rigorous rules about mirage structure. Folding and pleating the inner sphere while maintaining its smoothness allows us to transform the mirage into the original object, unveiling the constraints and possibilities imposed by topology.

The Magic of Degrees and Orientation

Degrees and orientation are key factors in understanding mirages. Each point on the object sphere corresponds to points on the image sphere that can be either inverted or erect. The degree of a mirage is determined by subtracting the number of inverted points from the number of erect points. Remarkably, topology reveals that the degree must be consistent throughout the sphere, leading to the conclusion that mirages always have a degree of one. This finding explains why mirages often exhibit alternating patterns of inverted and erect images.

Another intriguing result derived from topology is the odd number theorem. Complete mirages, including the "real" erect image of the object, always consist of an odd number of images. However, in most inferior mirages, where only one inverted image is visible below the real one, additional images are interrupted by nearby ground or other obstacles. This interruption disrupts the smooth and continuous transfer mapping between the image and object spheres, preventing further images from becoming visible.

Compression and Magnification: Mirage Effects

Mirage components can vary in visibility depending on their magnification or compression. The finite angular area of the image sphere imposes limitations on how many mirage images can be accommodated. As a result, some images become compressed and less noticeable, as observed in Mark's mirage where the tank images appear vertically compressed compared to the original.

Conversely, at folds on the image sphere, mirage images can be locally magnified. This magnification leads to vertical stretching in certain parts of the mirage, making phenomena like the green flash more visible. These effects highlight the intricate interplay between topology and mirage characteristics, shaping the visual spectacle we witness.

The Power of Playful Musing

The application of topology to mirages provides profound insights into their nature and behavior. Transparent rubbery balloons pressed against the inner surface of the object sphere offer a playful yet enlightening analogy. Through these imaginative musings, we gain a deeper understanding of the alternating patterns of erect and inverted images, the odd number theorem governing complete mirages, and the compression and magnification of mirage components.

Topology serves as a guiding framework, revealing the mirages we can expect to encounter and those that remain beyond our perception. Its abstract arguments ultimately translate into practical knowledge, enabling us to unravel the secrets of mirages and appreciate the intricate beauty they unveil in our atmosphere.

So next time you witness a mirage, remember the hidden world of topology that underlies its mesmerizing illusions.

Topology & Mirages

Mark Evans saw this very unusual mirage over the dry estuary sands of Swansea Bay, Wales. There are multiple images of the 7km distant gas storage tanks.

The sloping steps reveal the orientation of each mirage component. They alternate between inverted and erect.

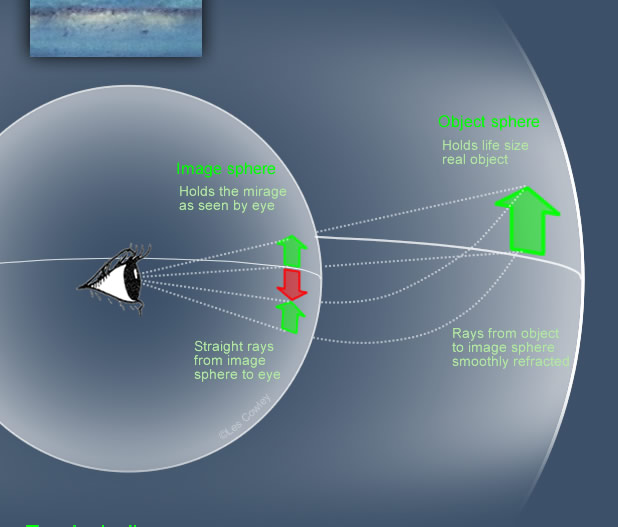
Topologically mirages can be represented by what we see pasted on a transparent inner 'image sphere' with the object pasted on a larger 'object sphere'.

The mirage from the inner sphere can be transformed into the object and vica-versa.

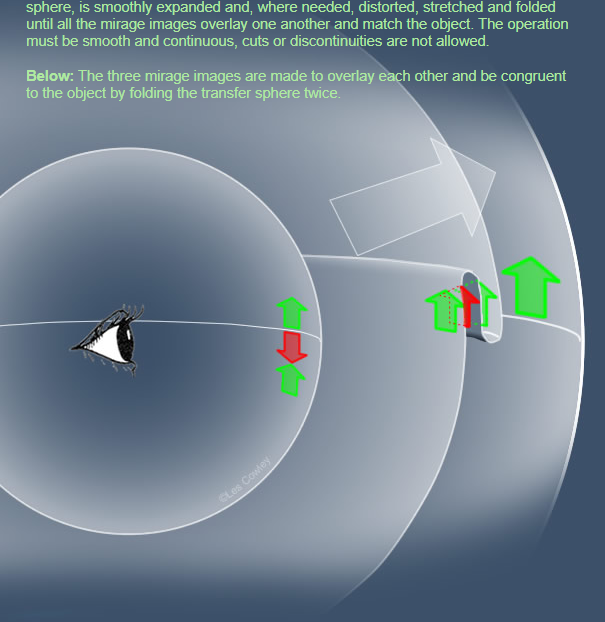
To do so the inner sphere, or a rubbery copy of it which we could call the transfer sphere, is smoothly expanded and, where needed, distorted, stretched and folded until all the mirage images overlay one another and match the object. The operation must be smooth and continuous, cuts or discontinuities are not allowed.

Below: The three mirage images are made to overlay each other and be congruent to the object by folding the transfer sphere twice.

Look at the sloping steps around the left-hand tank. They angle downwards from right to left. The mirage image immediately beneath it has the steps sloping in the opposite direction. The first mirage image is inverted.

We expect that. In a usual �inferior mirage�, a single upside-down image is below (inferior to) the miraged object. Light waves refracted at the boundary between warm air overlain by cooler air create it.

But Mark Evans' mirage is far more interesting! Beneath the first inverted image we see the ladder again. This time it slopes downwards in the same direction as on the real tank - this is an erect image! Below it are four or more images alternating inverted � erect � inverted � erect �

What is happening? We are actually seeing an unusually complete inferior mirage and the extensive, slightly undulating, warm sands have helped create it. The undulations have tilted the boundaries between the different temperature layers.

That does not entirely explain the multiple images nor why are they so neatly alternate inverted, erect, inverted? Answers come from topology and give unusual insight into mirage structure.

At left is a topological representation of a 3-image inferior mirage. What is seen is printed onto a nearby transparent sphere surrounding the eye. Further out is another sphere where the actual undistorted arrow is printed life size. The refraction and resulting curved rays are between the two spheres but we need not be concerned about temperature gradients or how or why the paths get curved. We simply look at the relations between the images on the two spheres.

Now for the magic. The mirage, no matter how complicated, pictured on the inner image sphere can nearly always be transformed into to the real object on the outer object sphere. To do so the inner sphere - or a copy of it - is smoothly and continuously expanded, where necessary distorting, folding or pleating (but never cutting or pasting) its rubbery surface until it meets the outer surface and the two sets of images exactly coincide. This is called transfer mapping.

The point of all this is that by mentally playing with these rubbery spheres we can derive rigorous rules about mirage structure, how their multiple images are oriented and how many images are possible.

At lower left, two folds transform the mirage into the original object. The limitations on how a surface might be folded hints at why mirage images alternate between inverted and erect but there is a more rigorous proof governing orientation.

The degree of the transformation relates the orientation of points on the two spheres. A point on the object sphere might have corresponding points on the image sphere that are inverted or erect. The degree is the number of erect points minus the number of inverted ones. For example, at left there are two erect points and one inverted for each object sphere point. The degree is 2-1=1

It is easy (at least after being shown how.!) to prove that the degree is has to be the same all over the sphere. Once that hurdle is out of the way it follows directly that mirages must always have a degree of one because there is nearly always part of the object sphere that is not miraged - that part has a degree of unity so the mirage itself must also have degree=1. These abstract arguments get us to a deep practical result. Mirages like erect, inverted, erect are allowed. Erect, erect, erect (for example) is not possible because its degree is not unity. Topology constrains the forms of mirages.

Another deep result, again easily.. derived, is the odd number theorem. Complete mirages always have an odd number of images if we include the �real� erect image of the object. But what of an �ordinary� inferior mirage with only one inverted image below the real one? Hence the qualification �complete�, in most inverted mirages the nearby ground interrupts rays that would otherwise form more images. The transfer mapping between the image and object spheres ceases to be smooth and continuous with some rays becoming tangent to the object sphere, a condition infringing the conditions for the theorems. More prosaically, the mirage ends before more images can become visible.

Mirage components can also be inconspicuous and unnoticed when they are demagnified. The angular area of the image sphere is finite yet it must hold the many mirage images. Is there always room? Some images become compressed and less visible. Notice how in Mark's mirage the tank images are vertically compressed compared to the original.

An opposite effect occurs at folds on the image sphere. There the image is locally magnified. Part of the mirage is vertically stretched. Fold stretching makes the green flash visible and may play a role in the vertical fantasies of the Fata Morgana.

Playful musing... about transparent rubbery balloons give deep insights into mirages. They tell us that upright and inverted images alternate, that complete mirages uninterrupted by ground or sea have an odd number of images, that parts can be magnified to blaze the beauty of a green flash, that parts compress into fine lines. Topology tells what mirages to search for and what we shall never see.

.

Think small rubber balloon pressed against the inside of the object sphere where there is an image and then where it is blank.

.. The degree for a smooth mapping must be one. I. e there is one more erect image than there are inverted ones. Therefore the total number of images must be 2.inverted +1, an odd number.

... Some of theory was developed to explain gravitational lensing and miraging of galaxies.

Thanks to Andrew Young for discussion and I am very much indebted to Walter Tape's article "The Topology of Mirages", Scientific American, 252, 120-129 (June 1985).

Images ©Mark Evans, shown with permission.

Note: this article has been automatically converted from the old site and may not appear as intended. You can find the original article here.

Reference Atmospheric Optics

If you use any of the definitions, information, or data presented on Atmospheric Optics, please copy the link or reference below to properly credit us as the reference source. Thank you!