Effect of drop size on primary rainbow
The Effect of Drop Size on the Primary Rainbow
When we look up at the sky after a heavy shower, we may notice a beautiful phenomenon known as a rainbow. Rainbows are formed when sunlight is refracted, or bent, as it passes through raindrops in the atmosphere. The primary rainbow, which is the most commonly observed rainbow, appears as a semi-circular band of colors with red on the outer edge and violet on the inner edge. But did you know that the appearance of the primary rainbow can vary depending on the size of the raindrops? In this article, we will explore the fascinating effect of drop size on the primary rainbow and delve into the underlying scientific principles.
The Relationship Between Drop Size and Rainbow Appearance
The appearance of a rainbow is closely linked to the size of the raindrops. Generally, narrower rainbows with intense and saturated colors are created by larger raindrops that measure several millimeters in diameter. These raindrops are most commonly observed during very heavy showers. On the other hand, smaller raindrops produce broader rainbows with less saturated colors. In fact, very small raindrops can even result in nearly colorless cloudbows and fogbows.
To better understand this relationship, let's take a look at an interesting example involving a lawn sprinkler. When the sprinkler is turned on, the drops of water it produces vary in size. As the water jet rotates, the drops near the main jet are larger and create a narrow and colorful bow. However, as the jet moves away and only smaller drops remain, the bow becomes broader and displays more pastel hues. This observation highlights the significant role that drop size plays in determining the appearance of the primary rainbow.
Explaining the Phenomenon
The classical theory of geometric optics, which treats light as rays, cannot fully explain the change in appearance and the dependence on drop size in rainbows. To understand this phenomenon, we need to consider the wave behavior of light. According to classical optics, each angle of the rainbow is composed of light that has traveled through raindrops along two different paths. The intensities of the two emerging rays are simply added together.
However, waves behave differently. If we represent the waves as alternate positive and negative crests along the classical ray paths, we find that the paths have different lengths. As a result, the crests can start in step as they travel towards the drop, but due to the different entrance points and path lengths, they can emerge from the drop out of step, creating a phase difference. This phase difference leads to interference between the waves, affecting their intensities.
The Role of Phase Difference and Interference
The interference of waves is crucial in understanding the changing appearance of the primary rainbow with varying drop sizes. As the drop size decreases, the phase difference between the two paths that form the rainbow oscillates more slowly with changes in angle. This leads to a broadening of the main rainbow peak and a wider spacing of any supernumerary rainbows that may appear within it.
Moreover, the color of the rainbow is also affected by drop size. The primary rainbow formed by sunlight is a combination of different monochromatic light bows. When the bows are broadened due to smaller drop sizes, the different colors overlap more, resulting in less saturated and more pastel hues.
Polarization and Other Considerations
While our discussion has focused primarily on the effect of drop size on the primary rainbow, it's important to note that other factors can influence its appearance as well. For instance, rainbows are polarized, meaning that the direction of the electric vibration within the light wave determines its polarization. This polarization affects the quantitative description of rainbows and fogbows, although it does not invalidate our qualitative explanation.
It's also worth mentioning that the simulations and observations discussed in this article are based on certain assumptions, such as a specific source size and uniform drop sizes. In reality, there is a distribution of drop sizes, and larger drops may be flattened to some extent, resulting in fewer visible supernumerary rainbows.
In conclusion, the effect of drop size on the primary rainbow is a captivating aspect of atmospheric optics. The appearance of the rainbow can vary from narrow and intense to broad and pastel, depending on the size of the raindrops. Understanding the wave behavior of light and the principles of interference helps explain these variations. Next time you spot a rainbow after a heavy shower, take a moment to appreciate the intricate interplay between drop size and the beauty of nature's colorful spectacle.
Primary Rainbow drop size

Lawn sprinkler bow, MSU Bozeman MT. As the jet rotated the bow width changed and the colours varied from bright and saturated colours to pastel hues. Image ©Les Cowley
A bow's appearance depends on drop size. The best are narrow ones with intense colours and these are made by large drops several mm in diameter. Look for them during very heavy showers.
Smaller drops produce broader bows with less saturated colours. Very small drops give nearly colourless cloudbows and fogbows.
The sprinkler's drops were largest near the main jet and they produced the narrow colourful bow. After the jet had rotated away and the large drops had fallen to earth the remaining smaller drops made the broader pastel bow.
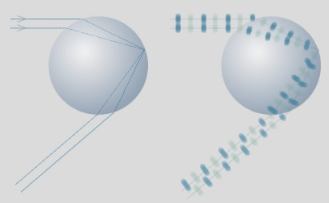
Classical geometric optics cannot explain the the change in appearance and dependence on drop size . We must invoke the wave behaviour of light.
Classically, each angle of the rainbow is made up of light that has traveled through drops along two different paths. Again classically, the two emerging ray intensities simply add together.
Classically, each rainbow angle has two ray paths. Their intensities add together. Representation of light waves along the paths. Positive and negative wave crests are dark and light blue. The light intensity from each path does not add because the wave crests are sometimes out of step.

AirySim computed rainbows for two drop sizes and for blue monochromatic light and sunlight.... As the drop size decreases the phase difference between the two rainbow forming ray (wave) paths oscillates more slowly with changes in angle. The diffraction pattern including the main bow broadens and the supernumeraries spread out.
Waves behave differently. Here. we can represent the waves as alternate positive and negative crests along the classical ray paths...
A critical feature is that the paths have different lengths. The crests start in step as they travel towards the drop but, as a consequence of the different entrance points and path lengths, they can emerge from the drop out of step - there is a phase difference.
The emergent wave intensities cannot simply be added because the waves interfere. When the crests are completely out of phase their positive and negative amplitudes cancel and there is little light, when in phase the light is intensified.
The phase difference and interference varies as the the rainbow deflection angle changes. The result is a peak in intensity near the classical rainbow angle with oscillatory fringes, supernumeraries, inside it.
The key to the changing appearance of the sprinkler bow is that as the drop size decreases the phase difference changes more slowly with angle. The main rainbow peak therefore broadens and any supernumeraries are more widely spaced.
Differences in colour with drop size? The sunlight bow is a superimposition of monochromatic light bows. When the bows are broadened, the different colours overlap more and the resultant hues are less saturated and pastel.
. This is diagrammatic but a reasonable representation for rainbow forming droplets 0.3mm dia. and upwards.
.. Light waves are transverse, the electric oscillations are at right angles to the wave travel. The direction of the electric vibration, the electric vector, determines the polarisation of the light. Unpolarised light has, over a short time period, electric vectors in all directions perpendicular to the ray direction. Pure plane polarised light has the electric vectors in a single direction. The intensity of light on being reflected or refracted depends on the direction of the initial polarisation relative to the surface. Rotate a pair of sunglasses while looking at a reflection in glass to show this. Rainbows are therefore polarised (rotate sunglasses while viewing one). Polarisation does not invalidate the above qualitative explanation but it does affect the quantitative description of rainbows and fogbows.
... The simulations are for a 0.5° diameter source, sun sized, and droplets all of one size. In nature, far fewer supernumeraries (if any) are visible because there is a distribution of drop sizes and larger drops are flattened to some extent.
Note: this article has been automatically converted from the old site and may not appear as intended. You can find the original article here.
Reference Atmospheric Optics
If you use any of the definitions, information, or data presented on Atmospheric Optics, please copy the link or reference below to properly credit us as the reference source. Thank you!
-
<a href="https://atoptics.co.uk/blog/effect-of-drop-size-on-primary-rainbow/">Effect of drop size on primary rainbow</a>
-
"Effect of drop size on primary rainbow". Atmospheric Optics. Accessed on July 27, 2024. https://atoptics.co.uk/blog/effect-of-drop-size-on-primary-rainbow/.
-
"Effect of drop size on primary rainbow". Atmospheric Optics, https://atoptics.co.uk/blog/effect-of-drop-size-on-primary-rainbow/. Accessed 27 July, 2024
-
Effect of drop size on primary rainbow. Atmospheric Optics. Retrieved from https://atoptics.co.uk/blog/effect-of-drop-size-on-primary-rainbow/.